 is given by the number of `carries' when we
add m and n-m in base p.
is given by the number of `carries' when we
add m and n-m in base p.
Many great mathematicians of the nineteenth century considered problems involving binomial coefficients modulo a prime power (for instance Babbage, Cauchy, Cayley, Gauss, Hensel, Hermite, Kummer, Legendre, Lucas and Stickelberger -- see Dickson). They discovered a variety of elegant and surprising Theorems which are often easy to prove. In this article we shall exhibit most of these results, and extend them in a variety of ways. We start with a discussion of what this article contains:
In 1852 Kummer showed that the power of prime p that divides the binomial
coefficient  is given by the number of `carries' when we
add m and n-m in base p.
is given by the number of `carries' when we
add m and n-m in base p.
In 1878 Lucas gave a method to easily determine
the value of  : Let
: Let 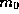 and
and 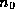 be the least
non-negative residues of m and
be the least
non-negative residues of m and  , respectively. Then
, respectively. Then
where, as usual, 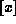 denotes the largest integer
denotes the largest integer 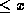 ,
and we use the convention
,
and we use the convention 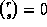 if r<s.
Re-writing
if r<s.
Re-writing 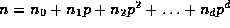 and
and
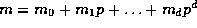 in base p
(so that
in base p
(so that 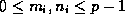 for each i), this may also be expressed
as
for each i), this may also be expressed
as

We will give three very different proofs of Lucas' Theorem: via number theory, via cellular automata, and via the combinatorics of power series.
Note that if p divides then (1) follows easily from Kummer's
Theorem. However, if
then (1) follows easily from Kummer's
Theorem. However, if 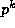 is the exact power of p dividing
is the exact power of p dividing  ,
then we might ask for the value of
,
then we might ask for the value of 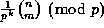 .
This is given by a result discovered by each of Anton (1869),
Stickelberger (1890) and Hensel (1902) (and many others since !), which
shows that
.
This is given by a result discovered by each of Anton (1869),
Stickelberger (1890) and Hensel (1902) (and many others since !), which
shows that
where r = n-m. Numerous authors have asked whether there is an analogous
formula, modulo 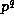 , for arbitrary
, for arbitrary 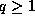 . In section 2 we show
the following:
For a given integer n define
. In section 2 we show
the following:
For a given integer n define  to be the product of those integers
to be the product of those integers
 that are not divisible by p.
that are not divisible by p.
Theorem 1. Suppose that prime power 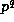 and positive integers
m=n+r are given. Let
and positive integers
m=n+r are given. Let 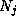 be the least positive residue of
be the least positive residue of 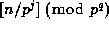 for each
for each 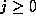 (and
make the corresponding definitions for m and r).
Let
(and
make the corresponding definitions for m and r).
Let 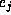 be the number of `carries', when adding m and r in base p,
on or beyond the jth digit). Then
be the number of `carries', when adding m and r in base p,
on or beyond the jth digit). Then
where 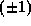 is
is 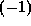 except if p=2 and
except if p=2 and 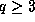 .
.
Taking q=1 in (3) gives (2).
Note that (3) may be re-written in terms of
factorials, since each 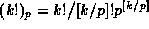 .
A similar result appears in
Davis and Webb .
.
A similar result appears in
Davis and Webb .
Theorem 1 provides a quick way to compute the value of binomial
coefficients modulo arbitrary prime powers: in fact
we will show
that this takes just 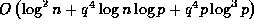 elementary operations.
elementary operations.
Wilson's Theorem (which was actually discovered by Liebnitz)
states that 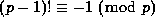 for all primes
p. An easy consequence of this is that
for all primes
p. An easy consequence of this is that
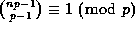 for all integers n.
In 1819 Babbage noticed that, further,
for all integers n.
In 1819 Babbage noticed that, further,
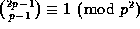 for all primes
for all primes 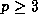 , and
Wolstenholme, in 1862, that
, and
Wolstenholme, in 1862, that
for all primes 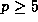 .
In 1952 Ljunggren generalized this to
.
In 1952 Ljunggren generalized this to
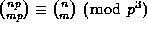 ;
and Jacobsthal to
;
and Jacobsthal to
for any integers n>m>0 and prime 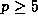 , where q
is the power of p dividing
, where q
is the power of p dividing 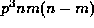 (this exponent q can only be increased if p divides
(this exponent q can only be increased if p divides 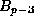 , the
, the
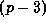 rd Bernoulli number).
These results, as well as many other similar congruences with larger
exponents q, follow easily from Proposition 5 below. For example,
if prime
rd Bernoulli number).
These results, as well as many other similar congruences with larger
exponents q, follow easily from Proposition 5 below. For example,
if prime 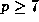 then
then
Ljunggren's result above may be re-written as
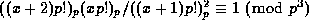 for any
integer
for any
integer
 and
and 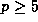 . Proposition 5 implies the generalization
. Proposition 5 implies the generalization
unless 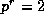 , or 2r+1 = p or
, or 2r+1 = p or 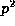 , when the congruence holds
, when the congruence holds
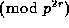 .
.
Another generalization of Wolstenholme's congruence is given by
Theorem 2. Suppose that prime p and positive integers u and r are given. Then
except if 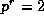 or 2r+1 = p or
or 2r+1 = p or 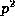 ,
when the congruence holds
,
when the congruence holds 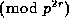 ,
where `
,
where `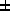 ' can only be `-' if p=2 (which is easily determined
by evaluating both sides of (8) modulo 4), and the integer
' can only be `-' if p=2 (which is easily determined
by evaluating both sides of (8) modulo 4), and the integer
Note how Theorem 2 allows us to express any  in terms of
in terms of 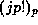 with
with 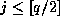 . In Theorem 3 below we prove
a similar result for any factorial, which allows us to compute such factorials
very rapidly.
. In Theorem 3 below we prove
a similar result for any factorial, which allows us to compute such factorials
very rapidly.
In 1899 Glaisher observed that the number of odd entries in any given
row of Pascal's Triangle is a power of 2. This follows from Kummer's
Theorem by noting that  is odd if and only if there
are no carries when adding m and n-m in base 2; in other words that
the digits `1' in the binary expansion of m are a subset of those in the
binary expansion of n. Clearly if there are k digits `1' in the
binary expansion of n, then there are
is odd if and only if there
are no carries when adding m and n-m in base 2; in other words that
the digits `1' in the binary expansion of m are a subset of those in the
binary expansion of n. Clearly if there are k digits `1' in the
binary expansion of n, then there are 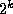 possible subsets of these
`1's, and each corresponds to a value of m -- thus there are
possible subsets of these
`1's, and each corresponds to a value of m -- thus there are 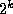 odd entries in the nth row of Pascal's Triangle.
odd entries in the nth row of Pascal's Triangle.
Larry Roberts also has an elegant (unpublished) result, depending on
Kummer's Theorem: Let 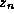 be the binary number whose mth digit
is
be the binary number whose mth digit
is 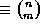 modulo 2; in other words, the integer formed
by reading the nth row of Pascal's Triangle, modulo 2, from left to right.
Then
modulo 2; in other words, the integer formed
by reading the nth row of Pascal's Triangle, modulo 2, from left to right.
Then 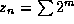 , where the sum is over those values of m, for
which the digits `1' in its binary expansion are a subset of those of n.
Thus if
, where the sum is over those values of m, for
which the digits `1' in its binary expansion are a subset of those of n.
Thus if 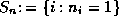 then
then
where 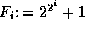 is the ith Fermat number.
is the ith Fermat number.
In section 5 we give somewhat different proofs of these results, and of Lucas' Theorem, using cellular automata.
In a recent paper , using methods from both elementary number theory
and the theory of cellular automata, we extended this result of
Glaisher's to the entries in Pascal's triangle that are 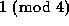 :
specifically we showed that in any given row of Pascal's triangle,
the number of entries that are congruent to
:
specifically we showed that in any given row of Pascal's triangle,
the number of entries that are congruent to 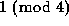 is either
0 or a power of 2. Similarly for
is either
0 or a power of 2. Similarly for 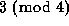 .
We then extended this to
.
We then extended this to 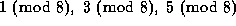 and
and 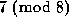 .
The likelihood of a general result of this type begins to emerge, and
to find out more the reader is encouraged to look at
my paper .
.
The likelihood of a general result of this type begins to emerge, and
to find out more the reader is encouraged to look at
my paper .
As is so well known, for any fixed n,
the sum, over all m, of the binomial coefficients
 , is exactly
2 to the power n. What is less well-known is that the
sum of the binomial coefficients, over all m in certain fixed
residue classes, sometimes satisfy certain
surprising congruences.
, is exactly
2 to the power n. What is less well-known is that the
sum of the binomial coefficients, over all m in certain fixed
residue classes, sometimes satisfy certain
surprising congruences.
In 1895 Morley showed that for any prime  ,
,
His ingenious proof, which is based on an explicit form of
De Moivre's Theorem, can be modified
to show that (14) holds modulo 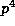 if and only if p divides
if and only if p divides 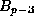 ;
however it cannot be modified to investigate other binomial coefficients,
and so we use different method for this in section 9. Our first result is
that
;
however it cannot be modified to investigate other binomial coefficients,
and so we use different method for this in section 9. Our first result is
that
for any 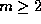 : In fact, this product is
: In fact, this product is 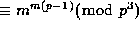 whenever the p-2nd Bernoulli polynomial vanishes
whenever the p-2nd Bernoulli polynomial vanishes 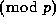 at
at
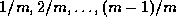 (which is immediate for m=2).
(which is immediate for m=2).
In 1938 Emma Lehmer related the values of
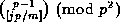 , for
, for  , to
Fermat's Last Theorem for exponent p. We shall show, in section 9, that
recent, as yet unpublished, results of Skula and Cui-Xiang imply that if
the first case of Fermat's Last Theorem is false for prime exponent p
(that is, there exist integers a, b, c, not divisible by p, for which
, to
Fermat's Last Theorem for exponent p. We shall show, in section 9, that
recent, as yet unpublished, results of Skula and Cui-Xiang imply that if
the first case of Fermat's Last Theorem is false for prime exponent p
(that is, there exist integers a, b, c, not divisible by p, for which
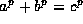 ) then
) then
for 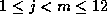 ; moreover, Skula'a approach implies that the `12'
here may be changed to any given number after a finite amount of computation.
; moreover, Skula'a approach implies that the `12'
here may be changed to any given number after a finite amount of computation.
There are many results in the literature that relate the value
of binomial coefficients of the form
 , for a given, fixed d>0
dividing p-1, to representations of the prime p by certain quadratic
forms (see Hudson and Williams). The first such result, due to Gauss (1828), is for d=4: \
Write any prime
, for a given, fixed d>0
dividing p-1, to representations of the prime p by certain quadratic
forms (see Hudson and Williams). The first such result, due to Gauss (1828), is for d=4: \
Write any prime 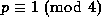 as
as 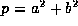 , and choose
the sign of a so that
, and choose
the sign of a so that 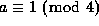 ; then
; then
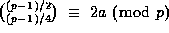 .
Recently, Beukers conjectured that
.
Recently, Beukers conjectured that

and this was proved by Chowla, Dwork and Evans.
In 1846, Jacobi showed that if we write any prime 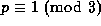 as
as 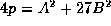 , where the sign of A is chosen so that
, where the sign of A is chosen so that
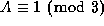 , then
, then
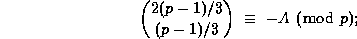
and this has now been shown to be  These congruences, modulo
These congruences, modulo 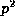 , have only been discovered quite
recently and there are presumably many others waiting to be found.
, have only been discovered quite
recently and there are presumably many others waiting to be found.