Further Reference Material
L.E. Dickson,
Divisibility of Factorials and Multinomial Coefficients,
Chapter XI in `History of the Theory of Numbers', Vol.I,
(Chelsea, New York, 1919).
W.J. Leveque,
Reviews in Number Theory (1945-1972), sections A08 and B64
(Amer. Math. Soc., Rhode Island, 1974).
R.K. Guy,
Reviews in Number Theory (1973-1983), sections A08 and B64
(Amer. Math. Soc., Rhode Island, 1984).
D. Singmaster,
Divisibility of binomial and multinomial
coefficients by primes and prime powers,
in `A collection of manuscripts related to the Fibonacci sequence',
(Fib. Assoc., Santa Clara, 1980), 98-113.
K.B. Stolarsky,
Power and Exponential sums of digit sums related to binomial coefficient parity,
SIAM J. Appl. Math., 32 (1977), 717-730.
Bibliography
Papers with results which we have not proved, or in which the
exposition is particularly elegant.
D.W. Boyd, J. Cook and P. Morton,
On sequences of 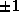 's defined by binary patterns,
's defined by binary patterns,
Diss. Math., 283, 60pp.
Neil Calkin,
A curious binomial identity,
Discrete Mathematics, 131 (1994), 335-337.
S. Chowla, B. Dwork and R. Evans,
On mod 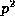 determination of
determination of 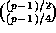 ,
,
J. of Number Theory, 24 (1986), 188-196.
K.S. Davis and W.A. Webb,
Lucas' Theorem for prime powers,
Europ. J. Combinatorics, 11 (1990), 229-233.
P. Erdös,
On a Diophantine Equation,
J. London Math. Soc. 26 (1951), 176-178.
P. Erdös and R.L. Graham,
On the prime factors of  ,
,
Fib. Quart. 14 (1976), 348-352.
P. Erdös and J.L. Selfridge,
The product of consecutive integers is never a power,
Illinois J. Math. 19 (1975), 292-301.
P. Erdös, C.B. Lacampagne and J.L. Selfridge,
Estimates of the least prime factor of a binomial coefficient
Math. Comp. 61 (1993) 215-224.
P. Erdös, R.L. Graham, I. Ruzsa and E.G. Straus,
On the prime factors of 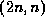 ,
,
Math. Comp. 29 (1975), 83-92.
R.D. Fray,
Congruence Properties of Ordinary and q-Binomial
Coefficients,
Duke Math. J., 34 (1967), 467-480.
J.B. Friedlander and J.C. Lagarias,
On the distribution
in short intervals of integers having no large prime factor,
J. Number Theory 25 (1987) 249-273.
R. Garfield and H.S. Wilf ,
The distribution of the binomial coefficients modulo p,
J. of Number Theory.
I. Gessel,
Some Congruences for the Apéry numbers,
J. of Number Theory, 14 (1982), 362-368.
P. Goetgheluck,
On prime divisors of binomial coefficients,
Math. Comp. 51 (1988), 325-329.
P. Goetgheluck,
Computing binomial coefficients,
Amer. Math. Monthly 94 (1987), 360-365.
C. Goldbach, letter to D. Bernoulli, July 23rd, 1724.
A. Granville,
Zaphod Beeblebrox's brain and the fifty-ninth row of Pascal's Triangle,
Amer. Math. Monthly, 99 (1992), 318-331.
Andrew Granville,
On the scarcity of powerful binomial coefficients.
R.H. Hudson and K.S. Williams,
Binomial Coefficients and Jacobi Sums,
Trans. Amer. Math. Soc., 281 (1984), 431-505.
J.P. Jones, D. Sato, H. Wada and D. Wiens,
Diophantine representation of the set of prime numbers,
Amer. Math. Monthly, 83 (1976), 449-464.
M. Jutila,
On numbers with a large prime factor,II,
J. Indian Math. Soc. 38 (1974) 125-130
D. E. Knuth and H. S. Wilf,
The power of a prime that divides a generalized binomial coefficient,
J. reine angew. Math., 396 (1989), 212-219.
E. Lehmer,
On congruences involving Bernoulli numbers and the
quotients of Fermat and Wilson,
Annals of Math., 39 (1938), 350-360.
C. T. Long,
Pascal's triangle modulo p,
Fib. Quart.,
19 (1981), 458-463.
H.B. Mann and D.S. Shanks,
A neccessary and sufficient condition for primality, and its source,
J. of Comb. Theory Ser. A, 13 (1972), 131-134.
F. Morley,
Note on the congruence
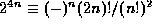 , where 2n+1 is a prime,
, where 2n+1 is a prime,
Annals of Math., 9 (1895), 168-170.
J. B. Rosser and L. Schoenfeld,
Approximate formulae for some functions of prime numbers,
Ill. J. Math. 6 (1962) 64-94.
J.W. Sander,
On prime power divisors of binomial coefficients,
Bull. London Math. Soc. 24 (1992) 140-142.
J.W. Sander,
Prime power divisors of binomial coefficients,
J. reine angew Math 430 (1992), 1-20.
J.W. Sander,
On primes not dividing binomial coefficients,
Proc. Camb. Phil, Soc. 113 (1993), 225-232.
J.W. Sander,
A story of binomial coefficients
and primes,
Amer. Math. Monthly 102 (1995), 802-807.
A. Sárközy,
On divisors of binomial coefficients I,
J. Number Theory 20 (1985) 70--80.
R. Scheidler and H.C. Williams,
A method of tabulating
the number-theoretic function 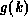 ,
,
Math. Comp. 59 (1992) 251-257.
G. Velammal,
Is the binomial coefficient 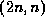 squarefree ?,
squarefree ?,
Hardy-Ramanujan Journal 18 (1995) 23-45.
S. Wagon and H.S. Wilf,
The
distribution of subset sums modulo m,
The
Electronic Journal of Combinatorics 1 (1994).
E.A. Wirsing,
Multiple prime divisors of binomial coefficients (to appear).
S. Wolfram,
Geometry of Binomial Coefficients,
Amer. Math. Monthly, 91 (1984), 566-571.
Some great books
Books which contain material used herein.
E. Bombieri,
Le grand crible dans la théorie analytique des nombres,
Astérisque 18 (1987/1974) 103 pp.
H. Davenport,
Multiplicative Number Theory
2nd ed. (Springer-Verlag, New York, 1980).
P. Erdös and R.L. Graham,
Old and new problems and results in combinatorial number theory,
Enseign. Math. Geneva (1980).
S.W. Graham and G. Kolesnik,
Van der Corput's Method of Exponential Sums,
(Cambridge University Press, Cambridge, 1991)
R.K. Guy,
Unsolved Problems in Number Theory,
2nd ed. (Springer-Verlag, New York, 1994).
H. Halberstam and H.-E. Richert,
Sieve Methods,
(Academic Press, London, 1974).
B. Mandelbrot,
The Fractal Geometry of Nature,
(Freeman, San Francisco, 1982).
E.C. Titchmarsh,
The Theory of the Riemann Zeta-function
2nd ed. (revised by Heath-Brown, D.R.), (Oxford U. Press, New York, 1988).
L.C. Washington,
Introduction to Cyclotomic Fields,
(Springer-Verlag, New York, 1982).
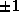 's defined by binary patterns,
's defined by binary patterns,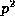 determination of
determination of 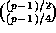 ,
, ,
,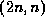 ,
,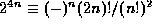 , where 2n+1 is a prime,
, where 2n+1 is a prime,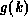 ,
, 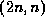 squarefree ?,
squarefree ?,