In (20) above we saw how any  may be expressed, modulo
may be expressed, modulo 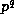 ,
in terms of values of
,
in terms of values of  with
with 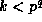 : this was
the key fact behind Proposition 1 and Theorem 1. In this section we
prove the following result which allows us to express
: this was
the key fact behind Proposition 1 and Theorem 1. In this section we
prove the following result which allows us to express 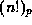 ,
modulo
,
modulo 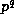 , in terms of
, in terms of  with k < qp:
Given integers
with k < qp:
Given integers  define
define
 .
.
Theorem 3. Suppose that prime power 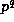 and non-negative
integers u and v are given with
and non-negative
integers u and v are given with 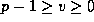 . Then
. Then
(21)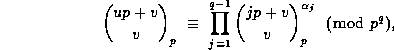
where the integer

Now, given  , where
, where 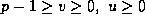 , first write
, first write
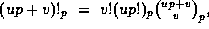 and then compute
and then compute  using Theorem 2, and
using Theorem 2, and 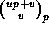 using
Theorem 3: We are thus able to express
using
Theorem 3: We are thus able to express 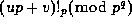 in terms of
in terms of 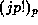 and
and  , with
, with 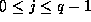 .
.
Notice that any 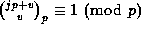 , so that
, so that
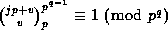 : Thus, in (21), we
need only consider the value of
: Thus, in (21), we
need only consider the value of  (and
similarly
(and
similarly
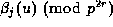 in (8)). Therefore, in order
to compute
in (8)). Therefore, in order
to compute 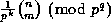 rapidly
(where k is as (2)), we suggest the following algorithm:\
rapidly
(where k is as (2)), we suggest the following algorithm:\
i) Use Theorem 1 to re-express 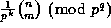 as a product of integers of the form
as a product of integers of the form 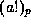 with
with 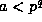 .
.
ii) Write each such a as up+v with  , and then
use Theorems 2 and 3 to write each such
, and then
use Theorems 2 and 3 to write each such 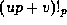 in terms of
in terms of
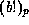 with b < qp, to powers no larger than
with b < qp, to powers no larger than  .
.
iii) Compute each  with b < qp, and then
take each of these to the required power.
with b < qp, and then
take each of these to the required power.
An elementary analysis reveals that (i) requires 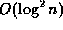 ,
(ii) requires
,
(ii) requires 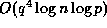 and (iii) requires
and (iii) requires 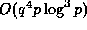 elementary operations, so that this algorithm typically produces enormous
savings over just using Theorem 1.
elementary operations, so that this algorithm typically produces enormous
savings over just using Theorem 1.
In order to prove Theorem 3, we need the following
Proposition 2. For any given prime power 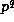 , integer
u and rational
y, whose denominator is not divisible by p, we have
, integer
u and rational
y, whose denominator is not divisible by p, we have
(22)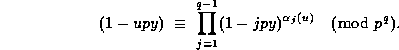
Theorem 3 then follows by taking the product of the equation in Proposition 2,
with 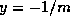 , for each
, for each 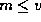 that is not divisble by p.
that is not divisble by p.
Henceforth let 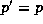 if
if 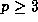 and
and 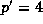 if p=2.
Eisenstein (1850) and Kummer (1851) introduced the p- adic logarithm
and p- adic exponential functions:
Given a rational number x, define p-adic numbers
if p=2.
Eisenstein (1850) and Kummer (1851) introduced the p- adic logarithm
and p- adic exponential functions:
Given a rational number x, define p-adic numbers
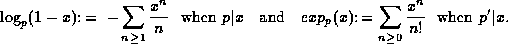
Various properties of these functions are discussed in section 5 of Washington's book:
For instance if p divides both x and y then
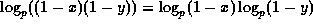 .
Moreover if
.
Moreover if 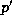 divides x then
divides x then  and
and
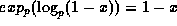 ;
also the highest power of p dividing x is the same as that dividing
;
also the highest power of p dividing x is the same as that dividing
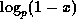 . These properties will be vital in our proofs of Theorems 2
and 3.
. These properties will be vital in our proofs of Theorems 2
and 3.
The Proof of Propositon 2: If  then the result is
trivial, so assume
then the result is
trivial, so assume 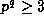 . Now take the p-adic logarithm of the
quotient of the two sides of (22), so that the result is equivalent to
proving that
. Now take the p-adic logarithm of the
quotient of the two sides of (22), so that the result is equivalent to
proving that
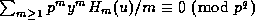 , where
, where
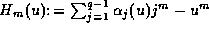 . We shall actually
prove that each individual term,
. We shall actually
prove that each individual term, 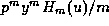 , of the sum is
, of the sum is
 . For those terms with
. For those terms with  we use
we use
Lemma 2. Given  and distinct
and distinct 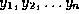 ,
we have
,
we have
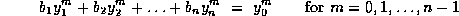
where
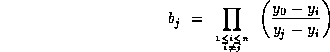
for each 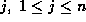 .
.
This may be verified in a number of ways, for instance by inverting the
relevant Vandermonde determinant.
Now, taking 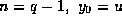 and each other
and each other 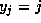 in Lemma 2, we find that
in Lemma 2, we find that
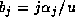 for each
for each 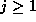 , and so
, and so
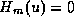 for
for 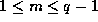 .
Note that each
.
Note that each 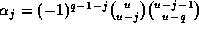 ,
and so is an integer.
,
and so is an integer.
For those terms with 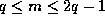 we use
we use
Lemma 3. Suppose that integers
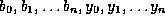 are given with
are given with
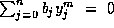 for
for 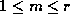 .
Then
.
Then  is divisible by m, whenever
is divisible by m, whenever
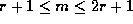 .
.
Proof: If 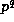 divides m then
divides m then 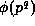 divides
divides 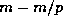 and
and
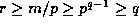 , so that
, so that
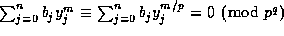 .
The result follows from the Chinese Remainder Theorem.
.
The result follows from the Chinese Remainder Theorem.
Thus taking 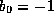 and, otherwise, the
and, otherwise, the  's and
's and 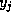 's as before,
we find that
's as before,
we find that
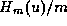 is an integer for
is an integer for 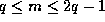 , by Lemma 3, and so
, by Lemma 3, and so
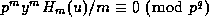 .
.
Finally note that the power of p dividing m is (trivially)  ,
so that the power of p dividing
,
so that the power of p dividing 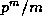 is
is 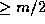 . Thus
. Thus
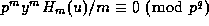 whenever
whenever 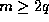 as
each
as
each 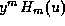 is an integer.
is an integer.
 may be expressed, modulo
may be expressed, modulo 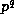 ,
in terms of values of
,
in terms of values of  with
with 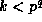 : this was
the key fact behind Proposition 1 and Theorem 1. In this section we
prove the following result which allows us to express
: this was
the key fact behind Proposition 1 and Theorem 1. In this section we
prove the following result which allows us to express 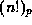 ,
modulo
,
modulo 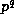 , in terms of
, in terms of  with k < qp:
Given integers
with k < qp:
Given integers  define
define
 .
.
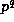 and non-negative
integers u and v are given with
and non-negative
integers u and v are given with 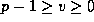 . Then
. Then
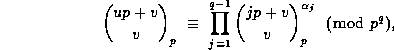

 , where
, where 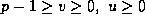 , first write
, first write
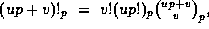 and then compute
and then compute  using Theorem 2, and
using Theorem 2, and 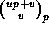 using
Theorem 3: We are thus able to express
using
Theorem 3: We are thus able to express 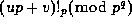 in terms of
in terms of 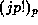 and
and  , with
, with 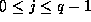 .
.
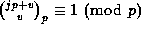 , so that
, so that
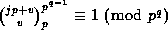 : Thus, in (21), we
need only consider the value of
: Thus, in (21), we
need only consider the value of  (and
similarly
(and
similarly
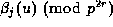 in (8)). Therefore, in order
to compute
in (8)). Therefore, in order
to compute 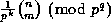 rapidly
(where k is as (2)), we suggest the following algorithm:\
rapidly
(where k is as (2)), we suggest the following algorithm:\
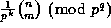 as a product of integers of the form
as a product of integers of the form 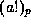 with
with 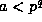 .
.
 , and then
use Theorems 2 and 3 to write each such
, and then
use Theorems 2 and 3 to write each such 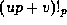 in terms of
in terms of
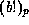 with b < qp, to powers no larger than
with b < qp, to powers no larger than  .
.
 with b < qp, and then
take each of these to the required power.
with b < qp, and then
take each of these to the required power.
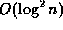 ,
(ii) requires
,
(ii) requires 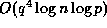 and (iii) requires
and (iii) requires 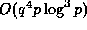 elementary operations, so that this algorithm typically produces enormous
savings over just using Theorem 1.
elementary operations, so that this algorithm typically produces enormous
savings over just using Theorem 1.
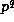 , integer
u and rational
y, whose denominator is not divisible by p, we have
, integer
u and rational
y, whose denominator is not divisible by p, we have
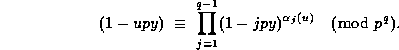
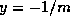 , for each
, for each 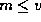 that is not divisble by p.
that is not divisble by p.
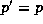 if
if 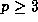 and
and 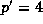 if p=2.
Eisenstein (1850) and Kummer (1851) introduced the p- adic logarithm
and p- adic exponential functions:
Given a rational number x, define p-adic numbers
if p=2.
Eisenstein (1850) and Kummer (1851) introduced the p- adic logarithm
and p- adic exponential functions:
Given a rational number x, define p-adic numbers
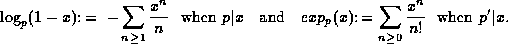
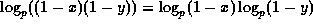 .
Moreover if
.
Moreover if 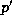 divides x then
divides x then  and
and
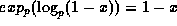 ;
also the highest power of p dividing x is the same as that dividing
;
also the highest power of p dividing x is the same as that dividing
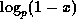 . These properties will be vital in our proofs of Theorems 2
and 3.
. These properties will be vital in our proofs of Theorems 2
and 3.
 then the result is
trivial, so assume
then the result is
trivial, so assume 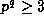 . Now take the p-adic logarithm of the
quotient of the two sides of (22), so that the result is equivalent to
proving that
. Now take the p-adic logarithm of the
quotient of the two sides of (22), so that the result is equivalent to
proving that
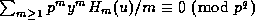 , where
, where
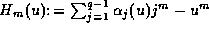 . We shall actually
prove that each individual term,
. We shall actually
prove that each individual term, 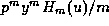 , of the sum is
, of the sum is
 . For those terms with
. For those terms with  we use
we use
 and distinct
and distinct 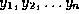 ,
we have
,
we have
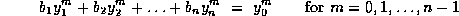
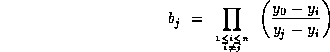
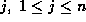 .
.
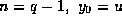 and each other
and each other 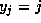 in Lemma 2, we find that
in Lemma 2, we find that
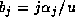 for each
for each 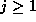 , and so
, and so
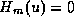 for
for 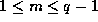 .
Note that each
.
Note that each 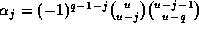 ,
and so is an integer.
,
and so is an integer.
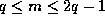 we use
we use
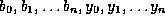 are given with
are given with
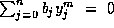 for
for 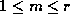 .
Then
.
Then  is divisible by m, whenever
is divisible by m, whenever
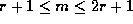 .
.
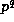 divides m then
divides m then 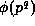 divides
divides 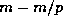 and
and
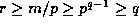 , so that
, so that
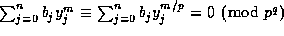 .
The result follows from the Chinese Remainder Theorem.
.
The result follows from the Chinese Remainder Theorem.
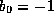 and, otherwise, the
and, otherwise, the  's and
's and 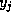 's as before,
we find that
's as before,
we find that
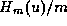 is an integer for
is an integer for 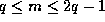 , by Lemma 3, and so
, by Lemma 3, and so
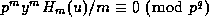 .
.
 ,
so that the power of p dividing
,
so that the power of p dividing 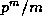 is
is 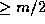 . Thus
. Thus
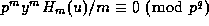 whenever
whenever 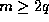 as
each
as
each 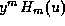 is an integer.
is an integer.