, is exactly
2 to the power n. What is less well-known is that the
sum of the binomial coefficients, over all m in certain fixed
residue classes, sometimes satisfy certain surprising congruences:
As is so well known, for any fixed n,
the sum, over all m, of the binomial coefficients
, is exactly
2 to the power n. What is less well-known is that the
sum of the binomial coefficients, over all m in certain fixed
residue classes, sometimes satisfy certain surprising congruences:
In 1876 Hermite showed that if n is odd then the sum of the binomial
coefficients , over those positive integers m that are
divisible by p-1, is divisible by p.
In 1899 Glaisher generalized this by showing that for
any given prime p and integers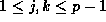 
, we have
for all positive integers 
.
In 1953 Carlitz generalized Hermite's Theorem to prime
powers: If 
divides n, with 
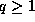and 
, then
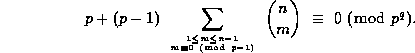
In 1913 Fleck gave the related result that for
any given prime p and integers 
, we have
where 
.
In 1965 Bhaskaran showed that if p is an odd prime then p+1 divides n if and only if
for 
.
