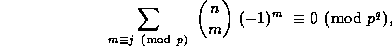
be a primitive p th root of unity and recall that
as ideals in Q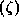
.
Define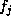 
to be the sum on the left side of (12) for each j, so that
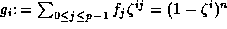which belongs to the ideal 
, for 
.
Therefore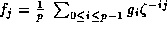 
,
belongs to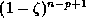 
, but as
each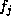 
is a rational integer, it is divisible by 
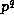where
is the smallest multiple of 
, which is 
,
and (12) follows immediately.