(34)
where the limit is taken p-adically.
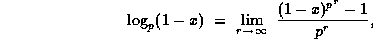
In section 11 we apply the results from here to binomial coefficients. We start by proving
Proposition 3. If x is divisible by prime p then
(34)
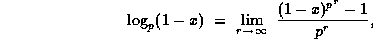
where the limit is taken p-adically.
Proof: Suppose that 
. If 
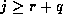then
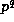divides the numerator of both 
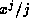and 
. If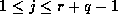 
and r is sufficiently large then
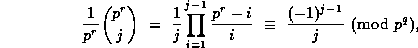
so that
Therefore, letting 
and then 
, we obtain (34).
For each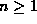 
, define
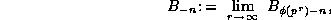
where the limit here is taken p-adically: Note that this limit
exists and is well defined by (29); moreover 
for all odd n.
(Using Theorem 5.11 of Washington's book, one can also show that
,
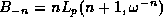where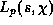 
is the p-adic L-function, and 
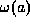is that
p-adic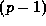 
st root of unity for which
.)
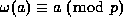Our main result of this section is
Proposition 4. For any integer x we have
(35)
where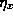 
(
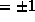) is chosen so that
, and
(Using Theorem 5.11 of Washington's book, one can also show that
,
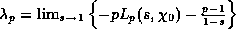where 
: note that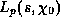 
has a pole at s=1.)
Proof: As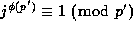 
whenever
p does not divide j, we have
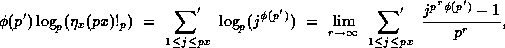
by Proposition 3. Now, fix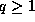 
and take 
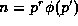in (30), so
that
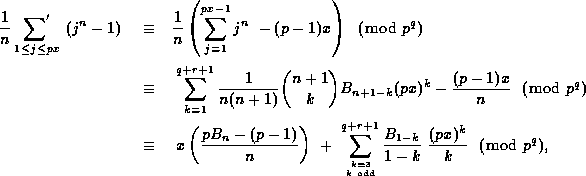
for all sufficiently large r, as
for those k in the sum.
Therefore, letting 
and then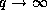 
, we obtain (35).