A Generalization of Lucas' Theorem.
For a given integer n define  to be the product of those integers
to be the product of those integers
 that are not divisible by p. We write
that are not divisible by p. We write  in base p,
and let
in base p,
and let 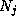 be the least positive residue of
be the least positive residue of 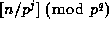 for each
for each 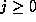 , so that
, so that  . Finally we
let
. Finally we
let  be the number of
`carries' on or beyond the jth digit, when adding m and r in base p.
be the number of
`carries' on or beyond the jth digit, when adding m and r in base p.
Theorem 1. For any prime power 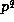 and positive integers m=n+r, we have
and positive integers m=n+r, we have
(3)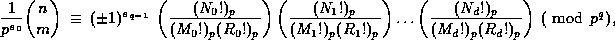
where 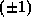 is
is 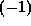 except if p=2 and
except if p=2 and 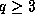 .
.
Now, with definitions as in Theorem 1, we have, for any given  ,
,

by
(20) .
.
Multiplying together this congruence for each  we get
we get
Proposition 1. For any integer n and prime power  ,
we have
,
we have

where  is defined as in Lemma 1 and each
is defined as in Lemma 1 and each  as in Theorem 1.
as in Theorem 1.
Theorem 1 then follows from dividing the equation in Proposition 1 by
the corresponding ones for m and r, and then using (19) to sort
out the exponents of  and p.
and p.
 to be the product of those integers
to be the product of those integers
 that are not divisible by p. We write
that are not divisible by p. We write  in base p,
and let
in base p,
and let 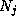 be the least positive residue of
be the least positive residue of 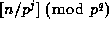 for each
for each 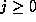 , so that
, so that  . Finally we
let
. Finally we
let  be the number of
`carries' on or beyond the jth digit, when adding m and r in base p.
be the number of
`carries' on or beyond the jth digit, when adding m and r in base p.
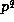 and positive integers m=n+r, we have
and positive integers m=n+r, we have
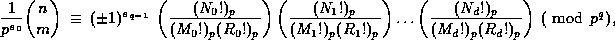
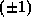 is
is 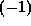 except if p=2 and
except if p=2 and 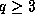 .
.
 ,
,

 .
. we get
we get
 ,
we have
,
we have

 is defined as in Lemma 1 and each
is defined as in Lemma 1 and each  as in Theorem 1.
as in Theorem 1.
 and p.
and p.