 .
A typical integer
.
A typical integer  has
has  digits, half of
which one expects to be 1's, so that
digits, half of
which one expects to be 1's, so that 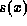 should be
approximately
should be
approximately 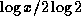 . Therefore, we compare
. Therefore, we compare 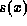 with
with
 , when
, when 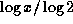 and
and 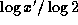 have the same
fractional part, by considering the function
have the same
fractional part, by considering the function
In 1968, Trollope proved the following result:
Let  .
A typical integer
.
A typical integer  has
has  digits, half of
which one expects to be 1's, so that
digits, half of
which one expects to be 1's, so that 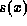 should be
approximately
should be
approximately 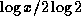 . Therefore, we compare
. Therefore, we compare 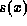 with
with
 , when
, when 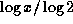 and
and 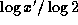 have the same
fractional part, by considering the function
have the same
fractional part, by considering the function
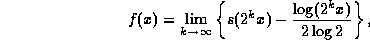
for each 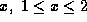 .
One can easily show that this limit exists and
that the function
.
One can easily show that this limit exists and
that the function 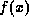 is continuous. However Trollope
proved the surprising result that
is continuous. However Trollope
proved the surprising result that 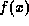 is nowhere differentiable.
For more on such questions see the paper by Boyd, Cook and Morton.
is nowhere differentiable.
For more on such questions see the paper by Boyd, Cook and Morton.