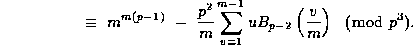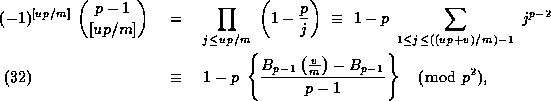
Taking n = p-1 in (31) gives
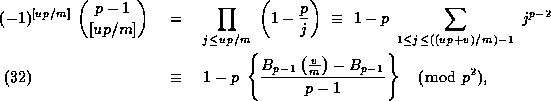
which implies (15) after summing over each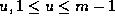 
,
applying (28) and then using Fermat's Theorem and the Von Staudt--Clausen
Theorem.
In 1909, Wieferich showed that if the first case of Fermat's Last
Theorem is false for prime exponent p then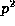 
divides 
;
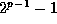thus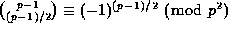 
by (15).
In 1914, Frobenius gave an induction hypothesis which should allow one to
extend this to 
divides 
, for each successive integer m;
however, because of the enormous amount of computation required for each
step of the hypothesis, this is currently known to hold only up to m=89.
In 1938, Emma Lehmer used identities like (28) to show that if the first case
of Fermat's Last Theorem is false for prime exponent p then
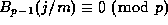for 
.
Recently Skula has modified Frobenius's induction hypothesis so that the
mth step might also show that
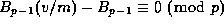for 
:
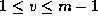(32) would then give (16) for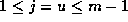 
.
(Skula has done this for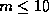 
; Zhong Cui--Xiang has obtained the same
result for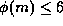 
, independantly.)
The left side of (15) is
(33)
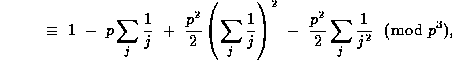
where 
.
Taking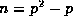 
and n=p-2 in (31), and then using a number of the
well--known congruences quoted in section 8 as well as (28), we obtain
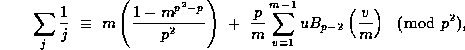
and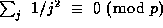 
.
Substituting these equations into (33), and using the fact that
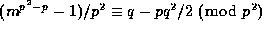for
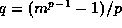, we see that the left side of (15) is
