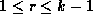 and
and
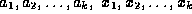 , with each
, with each 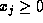 ,
are integers such that
,
are integers such that
The main result of this section is the most difficult of the paper:
Proposition 5. Suppose that 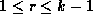 and
and
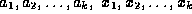 , with each
, with each 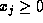 ,
are integers such that
,
are integers such that
(36)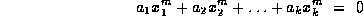
for each odd integer 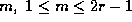 . Given
prime
p, let
. Given
prime
p, let
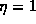 , unless p=2 and
, unless p=2 and 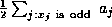 is odd, in which case
is odd, in which case 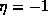 . Then
. Then
(37)
unless (i) 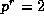 ; or
(ii) 2r+1=p and
; or
(ii) 2r+1=p and 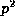 does not divide
does not divide  ; or
(iii)
; or
(iii) 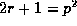 and p does not divide
and p does not divide 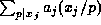 . In each of these three cases the congruence in
(36) holds
. In each of these three cases the congruence in
(36) holds  .
.
(Note that 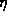 was chosen so that the left side of (37) is
was chosen so that the left side of (37) is
 .)
Proof of Theorem 2: Take
.)
Proof of Theorem 2: Take 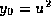 and each other
and each other 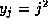 in Lemma 2, so that
in Lemma 2, so that  and thus
and thus
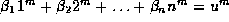 for each odd
for each odd
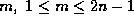 . Note that
. Note that
 , and so is an integer.
The result follows from taking r=n and k=n+1 in Proposition 5.
, and so is an integer.
The result follows from taking r=n and k=n+1 in Proposition 5.
Note that (6) follows from Theorem 2 with r=2 and u=3. We can also give the
Proof of (7): Take 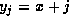 and n=2r
in Lemma 2 so that
and n=2r
in Lemma 2 so that
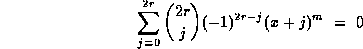
for each odd integer  . The result then follows
from taking k=2r+1 in Proposition 5.
. The result then follows
from taking k=2r+1 in Proposition 5.
Now assume that (36) holds for m=1. Proposition 4 then implies that
(38)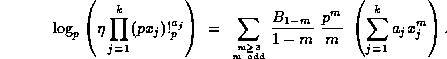
The idea will be to apply the p-adic exponential function 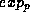 to both
sides of this equation.
For example, let
to both
sides of this equation.
For example, let 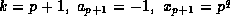 and
and
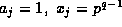 for
for  . Then (38) gives that
. Then (38) gives that
(39)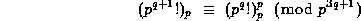
for 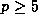 , and modulo
, and modulo 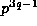 for p=2, 3 except if
for p=2, 3 except if 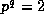 .
.
For another example let 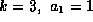 and
and 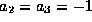 ,
so that
,
so that  ; note that this implies that
; note that this implies that
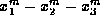 is divisible by
is divisible by 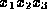 for all odd
for all odd  .
Jacobsthal's result (5) then follows easily from (38), as well as
a version for primes 2 and 3 ((5) holds if
.
Jacobsthal's result (5) then follows easily from (38), as well as
a version for primes 2 and 3 ((5) holds if  divides
divides 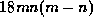 ).
).
We now proceed to the
Proof of Proposition 5: Start by noting that the proof of
Lemma 3 is easily modified to show that 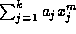 is divisible
by both
m-1 and m for all odd
is divisible
by both
m-1 and m for all odd 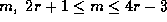 , given that (36)
holds for all odd
, given that (36)
holds for all odd 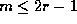 . Therefore, as each
. Therefore, as each 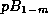 is a
p-adic unit, (38) implies that
is a
p-adic unit, (38) implies that
(40)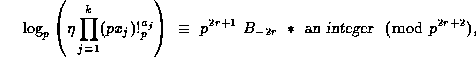
other than in those few cases where the terms for 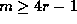 (in (38))
are relevant (namely for
(in (38))
are relevant (namely for 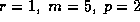 and 5, for
and 5, for
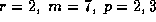 and 7, and for
and 7, and for 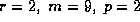 ; however they are
all
; however they are
all 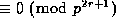 , except
, except 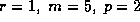 ).
).
Evidently the right side of (40) is 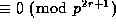 unless
p divides the denominator of
unless
p divides the denominator of  , in which case p-1 divides 2r,
by the Von Staudt-Clausen Theorem. For such cases we will prove
, in which case p-1 divides 2r,
by the Von Staudt-Clausen Theorem. For such cases we will prove
Lemma 4. In addition to the hypothesis of Proposition 5,
assume that p-1 divides 2r, and let 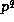 be the power of p that
divides
be the power of p that
divides 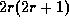 . Then
. Then 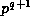 divides
divides 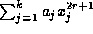 ,
except in cases (ii) and (iii) of Proposition 5.
,
except in cases (ii) and (iii) of Proposition 5.
p-1 divides 2r, except in cases (ii) and (iii); and Proposition 5 follows immediately.
From this deduce that p divides the integer in (40) whenever p - 1 divides 2r, except in cases (ii) and (iii); and Proposition 5 follows immediately.
It remains to give a
Proof of Lemma 4:
By hypothesis 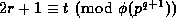 , where t=1 or
, where t=1 or 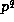 .
If 2r+1>t then
.
If 2r+1>t then  , and we are done. Clearly
, and we are done. Clearly
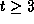 and so we may assume that
and so we may assume that 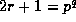 , which implies that
p is odd. If q=1 we get case (ii) so assume that
, which implies that
p is odd. If q=1 we get case (ii) so assume that 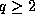 .
.
Now, if p does not divide a given integer x then
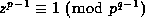 for
for 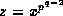 , so that
, so that
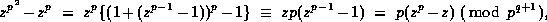
and thus
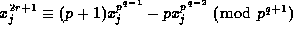 whenever p does not divide
whenever p does not divide 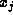 . This implies that
. This implies that
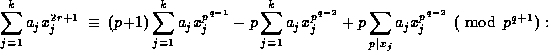
The first two sums here are 0 by (36) and the last is
 except in case (iii).
except in case (iii).